Q12

[ManhattanPrepLSAT1]

12. (B)
Question Type: Conditional
This question is similar to the second one we looked at. Since it’s asking us to find the maximum possible number of spaces between the first and second L, it makes sense to start with a six-space diagram, and to put L second and fifth (since it can’t go first or sixth):



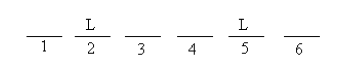
Now, just as we did on Question 8, we want to be sure to follow the inference chain. If L is second and fifth, who can go first and last? Let’s try both possibilities:





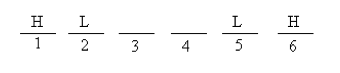
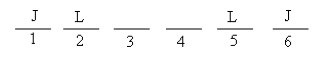
Do you see a problem? With positions two and five occupied, there’s nowhere for the HJ chunk to go! (This is where that "extra" inference from the setup reveals itself.) Clearly, there can’t be two spaces between the two L’s. Let’s try one space:



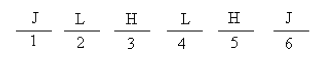
Yep, that works. Two is too many, but one is possible. Circle answer (B).

[al2568]

I solved this in a slightly different fashion.

I set up two diagrams: one starting with H, the other with J.

After plugging the 1 and 6 in, I satisfied the [HJ] requirement.

With J first, J_|_|_|HJ. Split the two L's with an H, get
J L H L H J.

With H first, HJ_|_|_|H. Split the two L's with a J, get
H J L J L H.