Did anyone draw frames for this game? at first i wrote the rules in tree form, then tried to combine...like
H-F-G--> K-J/L
or
G-F-H--> J-k/l
but i still ended up doing LOTS of frames, especially for 7, 9, & 10...
should I have drawn the frames to begin with or just stuck to the tree rules? i got most right, but it took awhile to draw out hypothethicals for most questions...any suggestions?
LSAT Forum
15 postsPage 1 of 1
-

- carmenmarrs
-
Thanks Received: 0
-
Vinny Gambini

- Posts: 6
- Joined: April 20th, 2009
-

- ManhattanPrepLSAT2
-
Thanks Received: 311
-
Atticus Finch

- Posts: 303
- Joined: July 14th, 2009
Re: pt 51, sect 4, game 2
I think you are smart for thinking of frames. Most relative ordering games don't require frames, but this one is certainly made easier by using them.
I've attached a diagram solution. Take a look, and let me know if you have any questions!
MK
I've attached a diagram solution. Take a look, and let me know if you have any questions!
MK
- Attachments
-
- PT51,S4,G2- Hotel Suites-ManhattanLSAT.pdf
- (50.52 KiB) Downloaded 816 times
-

- carmenmarrs
-
Thanks Received: 0
-
Vinny Gambini

- Posts: 6
- Joined: April 20th, 2009
Re: pt 51, sect 4, game 2
that was amazing! great diagram...now if i could only spot the right ones to do this type of split diagram with! My 1st diagram (after i wrote the rules-2ce the amount of time), was similar, but with this diagram I was able to do most questions without doing more frames...probably cut my time in half!
thanks so much!
thanks so much!
-

- velvet
-
Thanks Received: 0
-
Vinny Gambini

- Posts: 23
- Joined: October 03rd, 2011
Re: Diagram
Those 2 frames were genius! I have a habit of always writing the contrapositive for conditionals, so when I put down the contrapositives for the main 2 conditionals, I ended up confusing myself and wasn't able to clearly see the H-G & G-H sort of biconditional relationship going on. How come you didn't bother putting down the contrapositives in this one? I want to avoid making this mistake again. (I at least avoid writing the contrapositives for In/Out games except when necessary.) Thanks.
-

- hanselle.c
-
Thanks Received: 0
-
Vinny Gambini

- Posts: 6
- Joined: August 23rd, 2011
Re: Diagram
Just wondering - -
The Final rule resulting in F-G-H or G-F-H; how does this rule imply that we can't have H and G BEFORE (more expensive) than F?
Is it b/c the rule states an either/or+not both, and therefore any other alternative is ruled out?
I suppose I am to assume that this is always the case, for rules worded this way?
Thanks!!
The Final rule resulting in F-G-H or G-F-H; how does this rule imply that we can't have H and G BEFORE (more expensive) than F?
Is it b/c the rule states an either/or+not both, and therefore any other alternative is ruled out?
I suppose I am to assume that this is always the case, for rules worded this way?
Thanks!!
-

- noah
-
Thanks Received: 1192
-
Atticus Finch

- Posts: 1541
- Joined: February 11th, 2009
Re: Diagram
hanselle.c Wrote:Is it b/c the rule states an either/or+not both, and therefore any other alternative is ruled out?
I suppose I am to assume that this is always the case, for rules worded this way?
Exactly! It can't be more expensive than both. These sorts of rules do generally work out that something or somethings must be in the middle or on the outside. You can get some practice at that by playing our LSAT Arcade game "Draw It" - http://www.manhattanlsat.com/lsat-arcade.cfm
Have fun!
-

- jamiejames
-
Thanks Received: 3
-
Atticus Finch

- Posts: 116
- Joined: September 17th, 2011
Re: Diagram
Due to the last constrain, wouldn't I have to make 4 frames? For the G-H one depicting both F-G and F-H, and for H-G depicting both F-G and F-H?
-

- noah
-
Thanks Received: 1192
-
Atticus Finch

- Posts: 1541
- Joined: February 11th, 2009
- This post thanked 1 time.
Re: Diagram
jeastman Wrote:Due to the last constrain, wouldn't I have to make 4 frames? For the G-H one depicting both F-G and F-H, and for H-G depicting both F-G and F-H?
I think you may have misinterpreted the rule about F.
Before you read the last paragraph of this post, consider where it can fall in each situation: before both, in the middle, or after both:
G-H
H-G
Got it?
In both situations, the F must between the two elements. It can't come before (and after) both of them, only before (and after) one. Do you see why?
-

- jamiejames
-
Thanks Received: 3
-
Atticus Finch

- Posts: 116
- Joined: September 17th, 2011
Re: Diagram
noah Wrote:jeastman Wrote:Due to the last constrain, wouldn't I have to make 4 frames? For the G-H one depicting both F-G and F-H, and for H-G depicting both F-G and F-H?
I think you may have misinterpreted the rule about F.
Before you read the last paragraph of this post, consider where it can fall in each situation: before both, in the middle, or after both:
G-H
H-G
Got it?
In both situations, the F must between the two elements. It can't come before (and after) both of them, only before (and after) one. Do you see why?
ooooh I feel so silly now
-

- noah
-
Thanks Received: 1192
-
Atticus Finch

- Posts: 1541
- Joined: February 11th, 2009
Re: Diagram
jeastman Wrote:then it clicked and I had a huge "aha" moment. Thank you
Nice work. I thought you'd figure it out with a bit of prodding.
-

- tanner.lindsey.m
-
Thanks Received: 0
-
Vinny Gambini

- Posts: 1
- Joined: April 04th, 2011
Re: Diagram
Even with the diagram, I'm having a hard time with question #9. I can eliminate A and C, but what can't B or E be true?
-

- timmydoeslsat
-
Thanks Received: 887
-
Atticus Finch

- Posts: 1136
- Joined: June 20th, 2011

- Most Thanked

- First Responder
Re: Diagram
An ordering game with conditional statements. We really luck out with rules that allow us to infer the structure of the entire game.
During the rules, we are given a condition of G-H as well as a condition of H-G. These are the only possibilities in an ordering game.
So we can use all of the other rules given in the ordering game to make two ordering trees.
This is my global diagram:

There are two situations in this game and, for ease of communication, I labeled them 1 and 2.
1 = G-H situation
2 = H-G situation
Question 9 is a local question asking what could be true if we have L-F. As you can see, we will not be in situation 1, as this has F-L.
We can start with what we know, L-F, and use the ordering tree in situation 2 to make inferences.
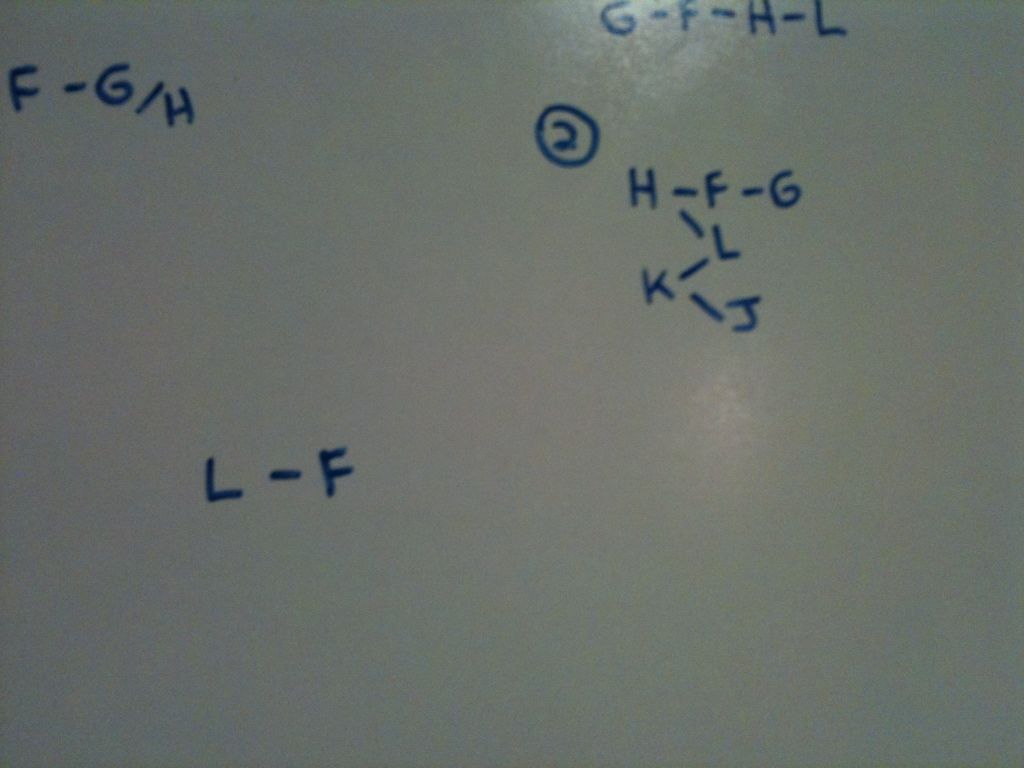
We know that G must follow F according to situation 2. We also know that H and K must precede L.
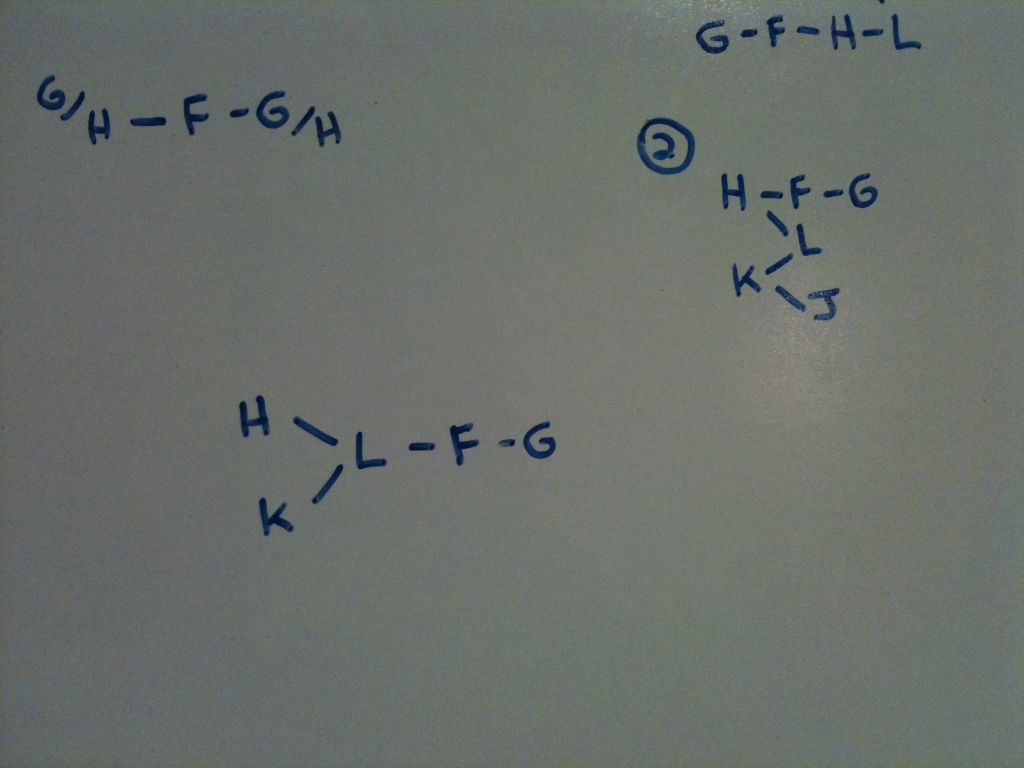
We also know that J must proceed K. (Get used to that kind of language!)
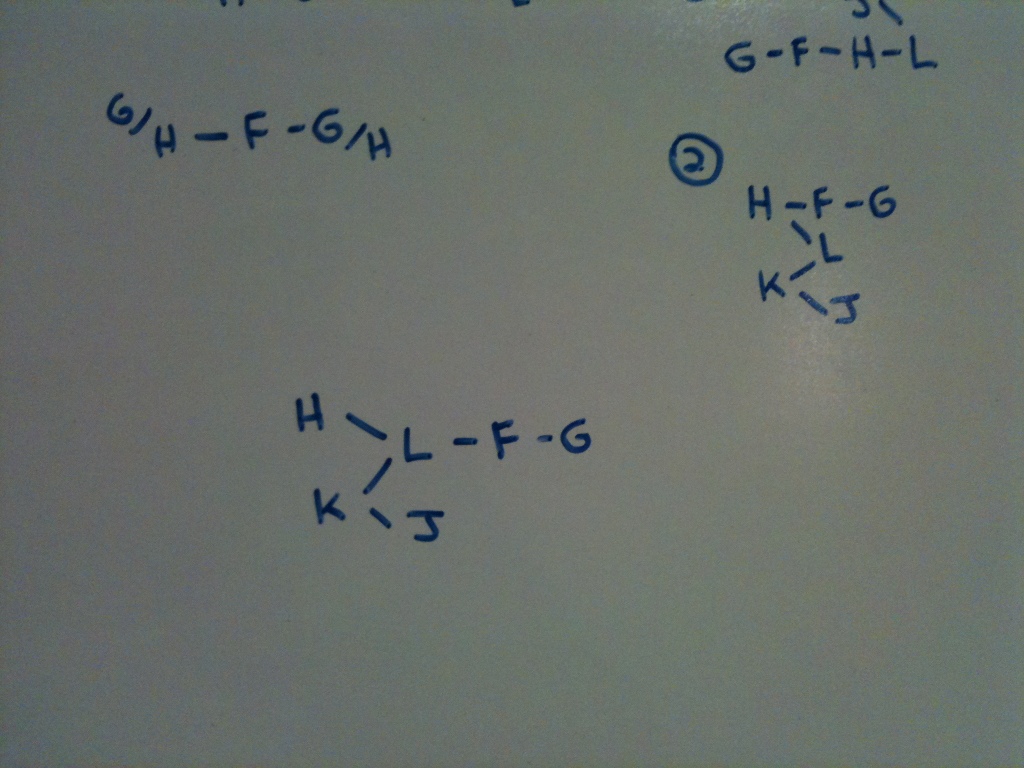
So this is what we have. As we can see G could certainly come prior to J.
During the rules, we are given a condition of G-H as well as a condition of H-G. These are the only possibilities in an ordering game.
So we can use all of the other rules given in the ordering game to make two ordering trees.
This is my global diagram:

There are two situations in this game and, for ease of communication, I labeled them 1 and 2.
1 = G-H situation
2 = H-G situation
Question 9 is a local question asking what could be true if we have L-F. As you can see, we will not be in situation 1, as this has F-L.
We can start with what we know, L-F, and use the ordering tree in situation 2 to make inferences.
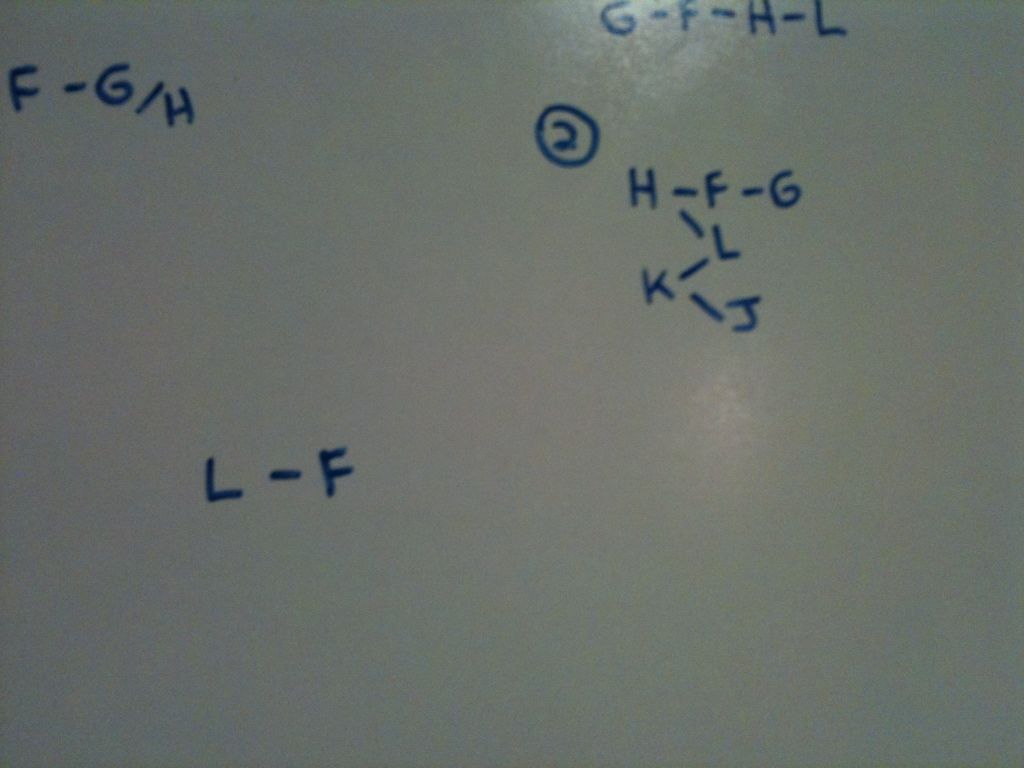
We know that G must follow F according to situation 2. We also know that H and K must precede L.
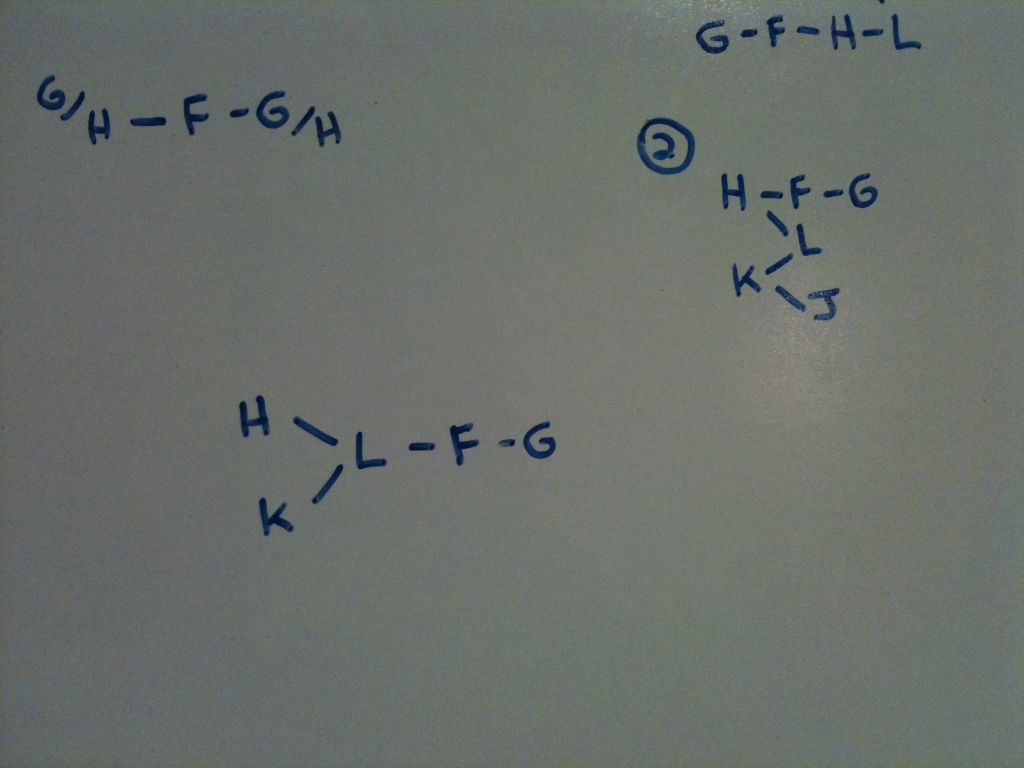
We also know that J must proceed K. (Get used to that kind of language!)
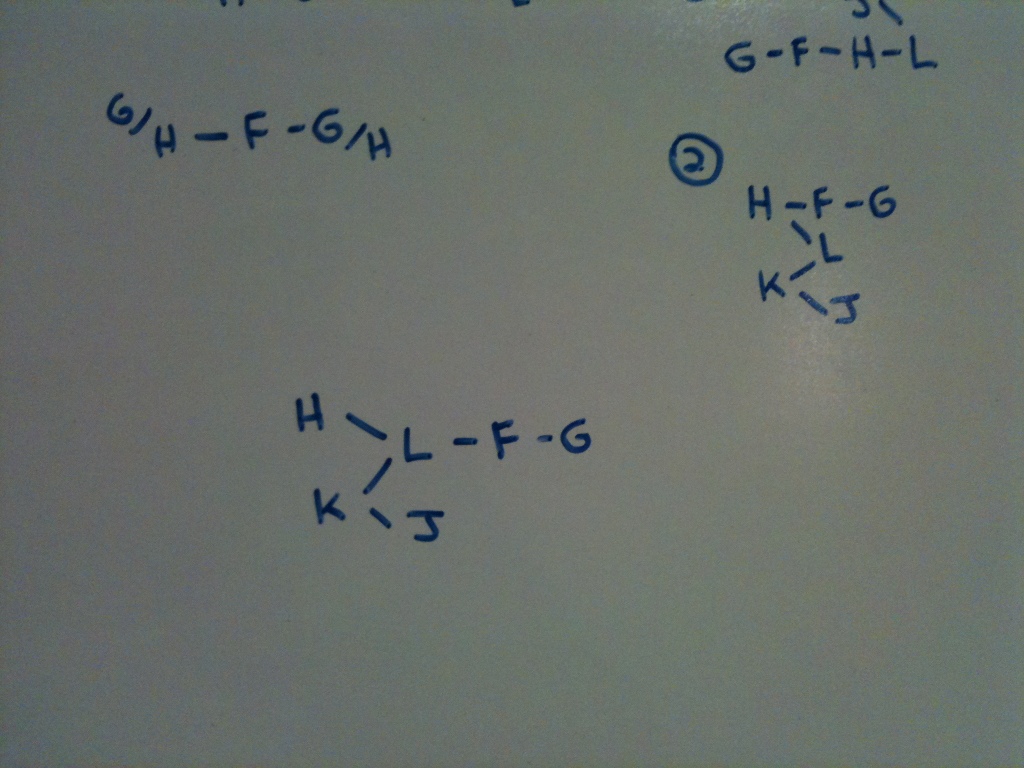
So this is what we have. As we can see G could certainly come prior to J.
-

- Amontillado
-
Thanks Received: 0
-
Vinny Gambini

- Posts: 7
- Joined: August 03rd, 2014
Re: Diagram
noah Wrote:hanselle.c Wrote:Is it b/c the rule states an either/or+not both, and therefore any other alternative is ruled out?
I suppose I am to assume that this is always the case, for rules worded this way?
Exactly! It can't be more expensive than both. These sorts of rules do generally work out that something or somethings must be in the middle or on the outside. You can get some practice at that by playing our LSAT Arcade game "Draw It" - http://www.manhattanlsat.com/lsat-arcade.cfm
Have fun!
Hi Noah, for the last rule, is it possible that F is LESS expensive than both G and H? It only excludes F-G,H, but could it be possible that G,H-F occurs?
Thank you : )
-

- Illogical_Historian
-
Thanks Received: 0
-
Vinny Gambini

- Posts: 1
- Joined: December 07th, 2014
Re: Diagram
Hi everyone,
I still don't understand how F can't be last after both G and H. I thought with "either/or not both" statements there was always a possibility that both statements could be false.
A---->/B
Or
B--->/A
You are either in Chicago or New York but not both.
Well can't it be the case that somebody is in neither Chicago or New York? I thought there was a possibility of neither A nor B occurring in an "either or but not both" scenario.
Is is because "or else" makes the outcome of the question one possibility? That is, if it is neither F <G or F <H as a possibility does that violate "or else." Can somebody help me see the errors of my ways?
Thanks.
I still don't understand how F can't be last after both G and H. I thought with "either/or not both" statements there was always a possibility that both statements could be false.
A---->/B
Or
B--->/A
You are either in Chicago or New York but not both.
Well can't it be the case that somebody is in neither Chicago or New York? I thought there was a possibility of neither A nor B occurring in an "either or but not both" scenario.
Is is because "or else" makes the outcome of the question one possibility? That is, if it is neither F <G or F <H as a possibility does that violate "or else." Can somebody help me see the errors of my ways?
Thanks.
-

- MatthiasJ110
-
Thanks Received: 0
-
Vinny Gambini

- Posts: 1
- Joined: September 18th, 2019
Re: Diagram
Hi,
I am having an issue with rule #4. I understand that F can either be more expensive than G, or H, but that F cannot be more expensive than both G and H. But what I don't understand is why G and H could not be BOTH more expensive than F at the same time. This possibility doesn't seem to be adressed by the rules.
Previous answers on this post have stated that rule #4 creates two frames : H-F-G and G-F-H. It makes sense that F can never be more expensive than both G and H, as it is stated by the rules. However, how do you know that H-G-F or G-H-F is impossible in this game ?
Thank you.
I am having an issue with rule #4. I understand that F can either be more expensive than G, or H, but that F cannot be more expensive than both G and H. But what I don't understand is why G and H could not be BOTH more expensive than F at the same time. This possibility doesn't seem to be adressed by the rules.
Previous answers on this post have stated that rule #4 creates two frames : H-F-G and G-F-H. It makes sense that F can never be more expensive than both G and H, as it is stated by the rules. However, how do you know that H-G-F or G-H-F is impossible in this game ?
Thank you.
15 posts Page 1 of 1