I have done this game several times and it keeps tripping me up. I did it pretty fast the 1st time & got 15-17 wrong, then it took me 10-12 min & I still got 15 & 17 wrong...my diagram was pretty much the same both times, so I'm wondering if I'm missing something or missing some inferences?
Any tips on the setup/ inferences would be greatly appreciated! I've heard this is one of those "repeat" type games, so I'd like to get it down...thanks so much!
LSAT Forum
10 postsPage 1 of 1
-

- carmenmarrs
-
Thanks Received: 0
-
Vinny Gambini

- Posts: 6
- Joined: April 20th, 2009
-

- dan
-
Thanks Received: 155
-
Atticus Finch

- Posts: 202
- Joined: March 10th, 2009
- This post thanked 1 time.
Re: pt 48, s2 g3 - In a repair facility there are exactly
Here's the basic setup for this game:
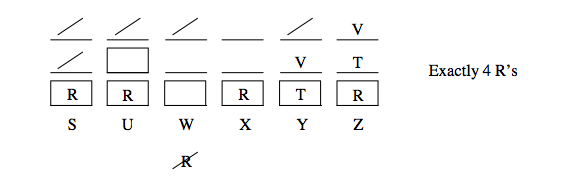
Hope it helps!
dan

Hope it helps!
dan
-

- JonT
-
Thanks Received: 0
-
Vinny Gambini

- Posts: 7
- Joined: March 01st, 2011
- Location: WA
Re: Diagram
got 15-17 wrong, then it took me 10-12 min & I still got 15 & 17 wrong.
Same here. Thanks a ton for the diagram and explanations, Dan - they were super helpful!
-

- timmydoeslsat
-
Thanks Received: 887
-
Atticus Finch

- Posts: 1136
- Joined: June 20th, 2011
- This post thanked 1 time.

- Most Thanked

- First Responder
Re: Diagram
I will post up my diagram and step by step explanation of it in the mean time.
We are told that there are 6 technicians and that each will perform at least one of three repairs.
So we do know that each technician must perform a repair, but we do not know as of now that every single repair will be used. In a situation like that, the inherent sense of order can be seen with the technicians being the base of the set up. We know each technician must have at least one repair, possibly all three. We simply do not know until we reach the rules.

The first rule tells us that X and three others do repair R.
Notice that I place the R with the X and I denote that I have three R's remaining to place. Five contenders for those three R's. We know X has repair R, but we do not know that it is ONLY R, it could be more.
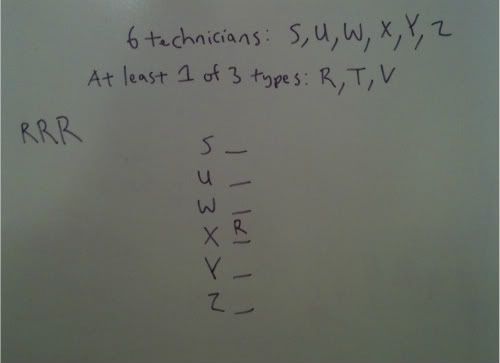
We know that Y does T and V. Y is not limited to those necessarily. We know that Y has those, but we do not know that it is ONLY those.

Our next rule tells us that S and Y do not share any repairs.
We only have three repair types: R, T, V.
We know that Y does T and V. That is 2 of the 3 repairs.
We know that each technician must do a repair. Since this rule tells us that S and Y share no repair in common, that means that S must have repair R. It also means that we can wall off Y and wall off S.
Those two technicians have their task lineup complete. There is no way that S could have any more repairs or that Y could. We also have one less R to worry about placing. We only have two R's left to place.

Our next rule tells us that Z repairs more than Y does. We know that Y must do 2 repairs. To have more repairs than Y it must do all three repairs. We can wall that off to show that this technician's selection is complete. We also have only one more R left to place.

Our next rule tells us that W and S do not share any repairs. We know that the only repair that S performs is R. Since W cannot do this repair, that means that the last R must be placed with U because there is no other place for this remaining R to go.

Our last rule tells us that U performs exactly two repairss.
We can wall off U with two repairs to be performed. We know that one of those repairs is R, so the other remaining one is one of T and V.
We know that W cannot do repair R, so the maximum amount of repairs it can do is two. We can wall off to show that it can only do 2 best case scenario. We know it must do one for sure, so I will show that with a slot, but I do not place a slot for a second repair because that is something that does not have to be true. I do know that W's task in that slot must be one of T and V.

Notice that X can have 1, 2, or 3 repairs.
U must have two, but we are not certain as to its makeup of that second repair.
We know that W's repair lineup consists of either 1 or 2 repairs.
The rest of the field is complete.
We are told that there are 6 technicians and that each will perform at least one of three repairs.
So we do know that each technician must perform a repair, but we do not know as of now that every single repair will be used. In a situation like that, the inherent sense of order can be seen with the technicians being the base of the set up. We know each technician must have at least one repair, possibly all three. We simply do not know until we reach the rules.

The first rule tells us that X and three others do repair R.
Notice that I place the R with the X and I denote that I have three R's remaining to place. Five contenders for those three R's. We know X has repair R, but we do not know that it is ONLY R, it could be more.
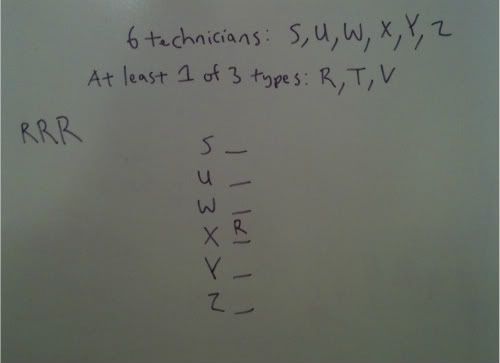
We know that Y does T and V. Y is not limited to those necessarily. We know that Y has those, but we do not know that it is ONLY those.

Our next rule tells us that S and Y do not share any repairs.
We only have three repair types: R, T, V.
We know that Y does T and V. That is 2 of the 3 repairs.
We know that each technician must do a repair. Since this rule tells us that S and Y share no repair in common, that means that S must have repair R. It also means that we can wall off Y and wall off S.
Those two technicians have their task lineup complete. There is no way that S could have any more repairs or that Y could. We also have one less R to worry about placing. We only have two R's left to place.

Our next rule tells us that Z repairs more than Y does. We know that Y must do 2 repairs. To have more repairs than Y it must do all three repairs. We can wall that off to show that this technician's selection is complete. We also have only one more R left to place.

Our next rule tells us that W and S do not share any repairs. We know that the only repair that S performs is R. Since W cannot do this repair, that means that the last R must be placed with U because there is no other place for this remaining R to go.

Our last rule tells us that U performs exactly two repairss.
We can wall off U with two repairs to be performed. We know that one of those repairs is R, so the other remaining one is one of T and V.
We know that W cannot do repair R, so the maximum amount of repairs it can do is two. We can wall off to show that it can only do 2 best case scenario. We know it must do one for sure, so I will show that with a slot, but I do not place a slot for a second repair because that is something that does not have to be true. I do know that W's task in that slot must be one of T and V.

Notice that X can have 1, 2, or 3 repairs.
U must have two, but we are not certain as to its makeup of that second repair.
We know that W's repair lineup consists of either 1 or 2 repairs.
The rest of the field is complete.
-

- shodges
-
Thanks Received: 0
-
Jackie Chiles

- Posts: 41
- Joined: August 23rd, 2011
Re: Diagram
I just don't get why the games is not grouped by what they can repair. Isn't it more efficient to group these in the smallest amount of groups possible?
-

- ManhattanPrepLSAT1
-
Thanks Received: 1909
-
Atticus Finch

- Posts: 2851
- Joined: October 07th, 2009
Re: Diagram
Good question shodges... The reason it's not best to group them by the type of machine they repair is that the rules are frequently about what the technicians repair in common and how many machines each repairs.
Suppose the game had 5 players and 3 teams. Each player was assigned to exactly one team. Regardless of whether you knew how many players went to each team, you'd want to organize the game by grouping the players into teams.
However in this game, we know neither how many machines each technician repairs nor how many technicians repair each type of machine. In this case, you should ask yourself, "which group has one or more of the other group?" The answer to that question will give you the most efficient organization. Since in this game each technician repairs one or more of the machines, we should use the technicians as the base.
Hope that clears up some of the confusion!
Suppose the game had 5 players and 3 teams. Each player was assigned to exactly one team. Regardless of whether you knew how many players went to each team, you'd want to organize the game by grouping the players into teams.
However in this game, we know neither how many machines each technician repairs nor how many technicians repair each type of machine. In this case, you should ask yourself, "which group has one or more of the other group?" The answer to that question will give you the most efficient organization. Since in this game each technician repairs one or more of the machines, we should use the technicians as the base.
Hope that clears up some of the confusion!
-

- jake.rambeau
-
Thanks Received: 2
-
Vinny Gambini

- Posts: 8
- Joined: November 24th, 2012
Re: Diagram
mattsherman Wrote:Good question shodges... The reason it's not best to group them by the type of machine they repair is that the rules are frequently about what the technicians repair in common and how many machines each repairs.
Suppose the game had 5 players and 3 teams. Each player was assigned to exactly one team. Regardless of whether you knew how many players went to each team, you'd want to organize the game by grouping the players into teams.
However in this game, we know neither how many machines each technician repairs nor how many technicians repair each type of machine. In this case, you should ask yourself, "which group has one or more of the other group?" The answer to that question will give you the most efficient organization. Since in this game each technician repairs one or more of the machines, we should use the technicians as the base.
Hope that clears up some of the confusion!
Matt,
This is exactly the kind of strategy I have been looking for, thank you! Can we assume the answer to that question will always give us the right base for open assignment games? Or are there other things to consider such as the rules. So I mean is there any possibility that the answer gives us "technicians" (just an example from this game), but then the rules are given in such a way that it actually makes more sense to do the opposite?
If that's possible, what are those things in the rules to look for?
-

- ca_teran1
-
Thanks Received: 2
-
Jackie Chiles

- Posts: 29
- Joined: May 23rd, 2012
Re: Diagram
Hello
I understand the game design
But how do you answer 13
Quickly?
Is the answer 2 because of y and z?
I understand the game design
But how do you answer 13
Quickly?
Is the answer 2 because of y and z?
-

- noah
-
Thanks Received: 1192
-
Atticus Finch

- Posts: 1541
- Joined: February 11th, 2009
Re: Diagram
ca_teran1 Wrote:Hello
I understand the game design
But how do you answer 13
Quickly?
Is the answer 2 because of y and z?
I know this is going to be annoying, but please post this in the Q13 thread. Otherwise this forum becomes a real mess. Thanks.
P.S. It looks like it was already explained there.
-

- andrewgong01
-
Thanks Received: 61
-
Atticus Finch

- Posts: 289
- Joined: October 31st, 2016
Re: Diagram
I disagree with the approach for this game and think grouping ity by R,T,V is easier and more efficient.
If we had it as rtv here's what we know :
R=X,Z,S,U
T=Y,Z
V=ZY
Then draw a cloud with VW and X over TV
Write down S can not go in T and V and W+Y can not go into R
This way all you ahve the track in the came is the cloud over TV so it is really limited
(Deductions I made from the rules to get what I had above)
X is in R and we have three spots left to fill for X
Y is in both T and V, since Z has to be greater than Y, Z is in all three of the groups. Now We have two spots left to fill for X
Since Y and S hate each other, (an anti chunk) we know that S has to go into group R Now we have one spot left to fill for X
Since S and W hate each other this implies that W has to be in either or both T + V ; who is left for R? We know that W+Y can not go in R and X,ZS are already in R so that means U is the only person left so it is U that goes to R -- R is now filled.
Since U has to appear twice, we draw a cloud for U to be in T and V
I think this is easier and more efficient to sort the game out than the current one above and I disagree with an earlier reasoning that doing it this way makes it harder to track since this game actaully is really limited unless there is something that i missed or done incorrectly this way? (my answers worked)
I t didn't seem like knowing the distribution was particularly useful in this game
If we had it as rtv here's what we know :
R=X,Z,S,U
T=Y,Z
V=ZY
Then draw a cloud with VW and X over TV
Write down S can not go in T and V and W+Y can not go into R
This way all you ahve the track in the came is the cloud over TV so it is really limited
(Deductions I made from the rules to get what I had above)
X is in R and we have three spots left to fill for X
Y is in both T and V, since Z has to be greater than Y, Z is in all three of the groups. Now We have two spots left to fill for X
Since Y and S hate each other, (an anti chunk) we know that S has to go into group R Now we have one spot left to fill for X
Since S and W hate each other this implies that W has to be in either or both T + V ; who is left for R? We know that W+Y can not go in R and X,ZS are already in R so that means U is the only person left so it is U that goes to R -- R is now filled.
Since U has to appear twice, we draw a cloud for U to be in T and V
I think this is easier and more efficient to sort the game out than the current one above and I disagree with an earlier reasoning that doing it this way makes it harder to track since this game actaully is really limited unless there is something that i missed or done incorrectly this way? (my answers worked)
I t didn't seem like knowing the distribution was particularly useful in this game
10 posts Page 1 of 1