LSAT Forum
6 postsPage 1 of 1
-

- ManhattanPrepLSAT1
-
Thanks Received: 1909
-
Atticus Finch

- Posts: 2851
- Joined: October 07th, 2009
-

- shaun_davis5
-
Thanks Received: 0
-
Vinny Gambini

- Posts: 9
- Joined: May 19th, 2014
Re: Diagram
On question 13-18, would it be possible to get breakdown of the questions and answers. During my timed section practice, I missed 17 and 18, but I would like to know "why" on the correct answers as well as the wrong answers.
Thanks
Thanks
-

- ManhattanPrepLSAT1
-
Thanks Received: 1909
-
Atticus Finch

- Posts: 2851
- Joined: October 07th, 2009
Re: Diagram
Solutions for each question are up!
-

- AubreyH4
-
Thanks Received: 0
-
Vinny Gambini

- Posts: 2
- Joined: May 10th, 2018
Re: Diagram
Solution is not up for Q12
-

- SamanthaW170
-
Thanks Received: 0
-
Vinny Gambini

- Posts: 7
- Joined: February 07th, 2018
Re: Diagram
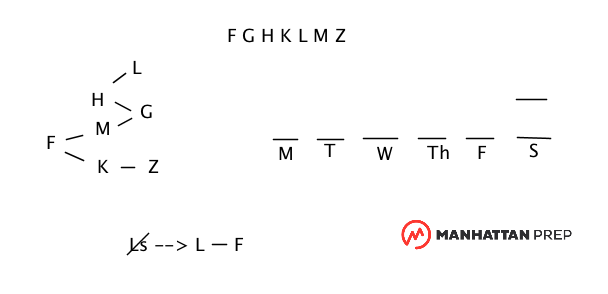
One of the rules for this game is that if L is not on Saturday, then L comes before F. The contrapositive of the statement is: If L is not before F (in this game, F-L, since F has to go in the beginning of the week, where it's not possible for two librarians to go on the same day), then L is on Saturday.
From the tree diagram, we see that there are four elements which have to go later in the week than F (and each has to go later in the week the one proceeding it on the chart): K-Z and M-G. This led to me conclude that F can only go on Monday or Tuesday, since K-Z and M-G need to go one each on Wednesday-Saturday.
From the diagram, we see that the only two librarians who could be on duty on Monday are F and H, since all other elements have at least one other element proceeding them.
I was thinking about these inferences, since both involve F, when I realized that if I am correct, is it ever possible for L to go before F? In other words, if F always has to go before L, then isn't L always on Saturdays?
Since the only option for the Monday librarian is F or H, if we put H first, F has to go on Tuesday, since it cannot go on Wednesday-Saturday. There would be no room for L before F.
It seems highly unlikely that a conditional rule could only play out one way in a game on the LSAT - where am I going wrong?
From the tree diagram, we see that there are four elements which have to go later in the week than F (and each has to go later in the week the one proceeding it on the chart): K-Z and M-G. This led to me conclude that F can only go on Monday or Tuesday, since K-Z and M-G need to go one each on Wednesday-Saturday.
From the diagram, we see that the only two librarians who could be on duty on Monday are F and H, since all other elements have at least one other element proceeding them.
I was thinking about these inferences, since both involve F, when I realized that if I am correct, is it ever possible for L to go before F? In other words, if F always has to go before L, then isn't L always on Saturdays?
Since the only option for the Monday librarian is F or H, if we put H first, F has to go on Tuesday, since it cannot go on Wednesday-Saturday. There would be no room for L before F.
It seems highly unlikely that a conditional rule could only play out one way in a game on the LSAT - where am I going wrong?
-

- ohthatpatrick
-
Thanks Received: 3808
-
Atticus Finch

- Posts: 4661
- Joined: April 01st, 2011
Re: Diagram
I think you're right that it will RARELY be the case that L - F, so it will USUALLY be the case that L is on Saturday.
But we can make L - F, given that tree, as long as we start with H.
Here's one such scenario:
H L F M G K Z
In any such scenario, we'd know that it starts
H L F
So it would have been prudent to frame this game based on whether L - F or F - L
Frame 1:
H L F M/K __ __ G/Z
Frame 2:
H/F __ __ __ __ __ L
Hope this helps.
But we can make L - F, given that tree, as long as we start with H.
Here's one such scenario:
H L F M G K Z
In any such scenario, we'd know that it starts
H L F
So it would have been prudent to frame this game based on whether L - F or F - L
Frame 1:
H L F M/K __ __ G/Z
Frame 2:
H/F __ __ __ __ __ L
Hope this helps.
6 posts Page 1 of 1